You've already forked Curso-lenguaje-C
Compare commits
9 Commits
3333040be4
...
main
| Author | SHA1 | Date | |
|---|---|---|---|
| af47cbdde7 | |||
| 6f7ac1cbcf | |||
| 29f903b286 | |||
| d24a4359ba | |||
| a4f9cf2e14 | |||
| bbb5ee43a5 | |||
| 49ba4fed2f | |||
| 9e79d0ffcd | |||
| 7a8e9b99f4 |
@@ -699,4 +699,6 @@ int main() {
|
||||
```
|
||||
|
||||
|
||||
[Volver arriba](#pec-1)
|
||||
[Volver arriba](#pec-1)
|
||||
|
||||
[Volver a la página principal de "Fundamentos de la Programación"](../README.md) | [Seguir a la PEC 2](../PEC2/README.md)
|
||||
|
||||
@@ -203,3 +203,5 @@ El puntero solo contiene la dirección inicial y el tipo es lo que nos permitir
|
||||
Hay que tener presente que el contenido de un puntero a entero es un entero y, por lo tanto, se puede asignar a una variable de tipo entero y se le puede aplicar cualquier operación entera, como por ejemplo, sumarle otro entero o escribirlo por pantalla. Lo mismo ocurre con cualquier otro tipo, o sea, el contenido de un puntero a real es un real y por lo tanto lo podemos tratar como tal.
|
||||
|
||||
[Volver arriba](#pec-2)
|
||||
|
||||
[Volver a la PEC1](../PEC1/README.md) | [Seguir a la PEC 3](../PEC3/README.md)
|
||||
|
||||
@@ -823,3 +823,5 @@ int main(int argc, char **argv) {
|
||||
Siempre se deben tomar precauciones, pero en especial cuando las cadenas de caracteres se crean dentro del programa, por ejemplo concatenando valores o distintas cadenas de caracteres, o cuando las introduce el usuario.
|
||||
|
||||
[Volver arriba](#pec-3)
|
||||
|
||||
[Volver a la PEC2](../PEC2/README.md) | [Seguir a la PR 1](../PR1/README.md)
|
||||
|
||||
@@ -662,3 +662,5 @@ Se deben crear solo los datos estructurados adecuados para el tratamiento de nue
|
||||
|
||||
|
||||
[Volver arriba](#pec-4)
|
||||
|
||||
[Volver a la PR1](../PR1/README.md) | [Seguir a la PR 2](../PR2/README.md)
|
||||
|
||||
@@ -663,3 +663,5 @@ Y ya podremos compilar y ejecutar el programa. Si todo ha ido bien, obtendremos
|
||||
|
||||
|
||||
[Volver arriba](#pec-5)
|
||||
|
||||
[Volver a la PR2](../PR2/README.md) | [Seguir a la PR 3](../PR3/README.md)
|
||||
|
||||
File diff suppressed because it is too large
Load Diff
311
fundamentos-programacion/PEC7/README.md
Normal file
311
fundamentos-programacion/PEC7/README.md
Normal file
@@ -0,0 +1,311 @@
|
||||
# PEC 7
|
||||
|
||||
[Volver a la página principal de "Fundamentos de la Programación"](../README.md)
|
||||
|
||||
**Índice**
|
||||
- [PEC 7](#pec-7)
|
||||
- [20. Recursividad](#20-recursividad)
|
||||
- [20.1. Ejemplo: números naturales](#201-ejemplo-números-naturales)
|
||||
- [20.2. Ejemplo: factorial](#202-ejemplo-factorial)
|
||||
- [20.3. Ejemplo: Tratamiento secuencial](#203-ejemplo-tratamiento-secuencial)
|
||||
- [20.3.1. Funciones auxiliares](#2031-funciones-auxiliares)
|
||||
- [20.3.2. Punteros](#2032-punteros)
|
||||
|
||||
|
||||
|
||||
|
||||
## 20. Recursividad
|
||||
|
||||
La recursividad es una técnica en programación donde una función se llama a sí misma para resolver problemas más pequeños de la misma naturaleza. Este enfoque es útil para problemas que pueden descomponerse en subproblemas más pequeños y similares. Sin embargo, es crucial manejar la recursividad con cuidado para evitar bucles infinitos o desbordamientos de pila.
|
||||
|
||||
|
||||
### 20.1. Ejemplo: números naturales
|
||||
|
||||
Los número naturales tienen su definición revursiva en matemáticas:
|
||||
|
||||
- 0 ∈ N
|
||||
- Si n ∈ N, entonces n+1 ∈ N
|
||||
|
||||
El conjunto de números naturales es el mínimo conjunto que cumple estas dos propiedades.
|
||||
|
||||
En este caso vemos que para definir qué es un número natural, lo hacemos recursivamente, o sea, a partir de saber que n es recursivo, sabemos que n + 1 también lo es. Con lo cual, lo podemos ver en el siguiente algoritmo:
|
||||
|
||||
```alg
|
||||
function isNatural(n: integer): boolean
|
||||
var
|
||||
result: boolean
|
||||
end var
|
||||
|
||||
if n = 0 then
|
||||
result := true
|
||||
else
|
||||
result := isNatural(n - 1)
|
||||
end if
|
||||
|
||||
return result
|
||||
|
||||
end function
|
||||
```
|
||||
|
||||
```c
|
||||
#include <stdbool.h>
|
||||
|
||||
bool isNatural(int n) {
|
||||
if (n == 0) {
|
||||
result = true;
|
||||
} else {
|
||||
result = isNatural(n - 1);
|
||||
}
|
||||
return result;
|
||||
}
|
||||
```
|
||||
|
||||
En este código vemos un ejemplo de los dos elementos que todo algoritmo recursivo debe tener:
|
||||
|
||||
- Condición de finalización (en este caso cuando n es 0)
|
||||
- Regla recursiva (una llamada recursiva con n-1)
|
||||
|
||||
En la siguiente figura se puede ver la simulación de lo que pasaría en la memoria cuando se llama `isNatural(2)`.
|
||||
|
||||
step 1 - Veremos que cuando se llama isNatural con el valor 2, este queda guardado en una zona de memoria.
|
||||
|
||||
```
|
||||
| ... | 32 | 33 | 34 | 35 | ... | 65 | 66 | 67 | 68 | ... | 215 | 216 | 217 | 218 | ... |
|
||||
|-----|----|----|----|-----|-----|----|----|----|----|-----|-----|-----|-----|-----|-----|
|
||||
| ... | 2 | ... | | | | | ... | | | | | ... |
|
||||
| ... | n | ... | | | | | ... | | | | | ... |
|
||||
```
|
||||
|
||||
step 2 - Siguiendo con el algoritmo, ya que n no es 0, se hace otra llamada a isNatural con el valor 1. Esta nueva llamada se añade a la pila y queda guardada en otra zona de memoria diferente. Como n todavía no es 0, se vuelve a hacer una llamada a isNatural con el valor 0 y esta nueva llamada también queda añadida a la pila utilizando otra zona de memoria.
|
||||
```
|
||||
| ... | 32 | 33 | 34 | 35 | ... | 65 | 66 | 67 | 68 | ... | 215 | 216 | 217 | 218 | ... |
|
||||
|-----|----|----|----|-----|-----|----|----|----|----|-----|-----|-----|-----|-----|-----|
|
||||
| ... | 2 | ... | 1 | ... | | | | | ... |
|
||||
| ... | n | ... | n | ... | | | | | ... |
|
||||
```
|
||||
|
||||
step 3 - En este caso, como el parámetro tiene valor 0, se devolverá un true y se finalizará esta llamada.
|
||||
```
|
||||
| ... | 32 | 33 | 34 | 35 | ... | 65 | 66 | 67 | 68 | ... | 215 | 216 | 217 | 218 | ... |
|
||||
|-----|----|----|----|-----|-----|----|----|----|----|-----|-----|-----|-----|-----|-----|
|
||||
| ... | 2 | ... | 1 | ... | 0 | ... |
|
||||
| ... | n | ... | n | ... | n | ... |
|
||||
```
|
||||
|
||||
step 4 - Cuando se finaliza la ejecución de una acción o función, toda la memoria ocupada por sus parámetros y variables se elimina y, por lo tanto, ahora solo quedarán las dos llamadas iniciales a la memoria.
|
||||
```
|
||||
| ... | 32 | 33 | 34 | 35 | ... | 65 | 66 | 67 | 68 | ... | 215 | 216 | 217 | 218 | ... |
|
||||
|-----|----|----|----|-----|-----|----|----|----|----|-----|-----|-----|-----|-----|-----|
|
||||
| ... | 2 | ... | 1 | ... | | | | | ... |
|
||||
| ... | n | ... | n | ... | | | | | ... |
|
||||
```
|
||||
|
||||
step 5 - La segunda llamada devolverá el valor true que ha devuelto la última llamada y, por tanto, finalizará y quedará solo la primera llamada a la memoria. Finalmente esta llamada inicial retornará y también se eliminará de la memoria.
|
||||
```
|
||||
| ... | 32 | 33 | 34 | 35 | ... | 65 | 66 | 67 | 68 | ... | 215 | 216 | 217 | 218 | ... |
|
||||
|-----|----|----|----|-----|-----|----|----|----|----|-----|-----|-----|-----|-----|-----|
|
||||
| ... | 2 | ... | | | | | ... | | | | | ... |
|
||||
| ... | n | ... | | | | | ... | | | | | ... |
|
||||
```
|
||||
|
||||
Lo importante es ver que, aunque sea la misma función, a efectos prácticos es como si se tratara de funciones diferentes y, por tanto, los parámetros y variables que tenga son independientes entre llamadas.
|
||||
|
||||
|
||||
### 20.2. Ejemplo: factorial
|
||||
|
||||
El factorial de un número n se define como el producto de todos los números enteros positivos desde 1 hasta n. Se denota n! y se define de la siguiente manera:
|
||||
|
||||
- n! = 1 x 2 x 3 x ... x (n-1) x n
|
||||
|
||||
Una posible función **factorial** con estructuras **iterativas** podría ser:
|
||||
|
||||
```alg
|
||||
function fact(n: integer): integer
|
||||
var
|
||||
i: integer
|
||||
f: integer
|
||||
end var
|
||||
|
||||
f := 1
|
||||
|
||||
for i := 1 to n do
|
||||
f := f * i
|
||||
end for
|
||||
|
||||
return f;
|
||||
|
||||
end function
|
||||
```
|
||||
|
||||
`unsigned` *es un modificador de tipo que indica que la variable no puede almacenar valores negativos. Esto es diferente de los tipos* `signed`*, que permiten tanto valores positivos como negativos.*
|
||||
|
||||
```c
|
||||
unsigned int fact(int n){
|
||||
unsigned int i = 0;
|
||||
unsigned int f = 1;
|
||||
|
||||
for (i = 1; i <= n; i++){
|
||||
f *= i;
|
||||
}
|
||||
|
||||
return f;
|
||||
|
||||
}
|
||||
```
|
||||
|
||||
Si lo pensamos de forma **recursiva**, podemos ver que factorial(n) es lo mismo que n x factorial(n-1). De esta manera podemos sustituir una función con iteraciones por una función recursiva que vuelve a si misma hasta que se cumple una condición de parada.
|
||||
|
||||
Por lo tanto:
|
||||
|
||||
```alg
|
||||
function fact(n:integer): integer
|
||||
var
|
||||
result: integer;
|
||||
end var
|
||||
|
||||
if n == 1 then
|
||||
result := 1;
|
||||
else
|
||||
result:= n * fact(n - 1);
|
||||
end if
|
||||
|
||||
return result;
|
||||
|
||||
end function
|
||||
```
|
||||
|
||||
```c
|
||||
unsigned int fact(unsigned int n){
|
||||
int result;
|
||||
|
||||
if (n == 1){
|
||||
result = 1;
|
||||
} else {
|
||||
result = n * fact(n - 1);
|
||||
}
|
||||
|
||||
return result;
|
||||
|
||||
}
|
||||
```
|
||||
|
||||
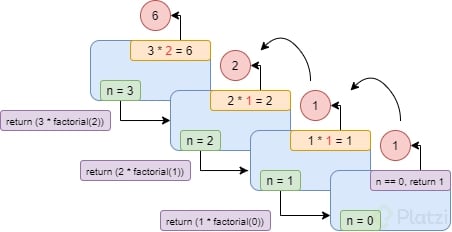
A continuación se muestra un esquema de lo que pasaría en la pila de programas (program stack) si
|
||||
hiciéramos una llamada a este método para `n = 3` dentro del programa principal `main`. De izquierda a derecha se
|
||||
muestra la evolución temporal, que corresponde a los siguientes pasos:
|
||||
1. En la pila solo está el `main`.
|
||||
2. Cuando desde el `main` se llama `fact(3)`, en la pila se hace un *push* de la información referente a la función `fact`. En este caso, el parámetro `n` tiene un valor de 3, que es lo que se le ha indicado en la llamada.
|
||||
3. Como `n` no tiene un valor igual a 1 se devuelve el resultado de la expresión `n * fact(n-1)*`. **Como el valor de** `n` **es 3, es necesario evaluar la expresión** `3 * fact(2)`**, y por tanto, se hace una llamada a la función** `fact` **pasando como parámetro el 2.**
|
||||
4. Al hacer la llamada a `fact(2)`, en la pila se hace un *push* de la información referente a la función `fact`, donde, en este caso, el parámetro `n` tiene un valor de 2.
|
||||
5. Como `n` no tiene un valor igual a 1 se devuelve el resultado de la expresión `n * fact(n-1)`. Como el valor de `n` es 2, hay que evaluar la expresión `2 * fact(1)`, y por tanto, hay que hacer una llamada a la función `fact` pasando como parámetro el 1.
|
||||
6. Como ahora `n` tiene un valor igual a 1, entra en el `if` y devuelve el valor 1. En el retorno se hace un *pop* de la pila, que elimina toda la información de la última función que se había añadido.
|
||||
7. Dado que ahora ya tenemos el valor de `fact(1)`, se puede evaluar la expresión `2 * fact(1)`, y se devuelve el valor 2. Cuando hacemos el retorno, se hace un *pop* de la pila, eliminando toda la información de la última función que se había añadido.
|
||||
8. Dado que ahora ya tenemos el valor de `fact(2)`, se puede evaluar la expresión `3 * fact(3)` y se devuelve el valor 6. En el retorno, se hace un *pop* de la pila, que elimina toda la información de la última función que se había añadido, y solo deja en la pila la información de la función `main`, que se eliminará cuando esta finalice.
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
### 20.3. Ejemplo: Tratamiento secuencial
|
||||
|
||||
En general, la mayoría de los algoritmos que tratan secuencias son susceptibles de ser formulados de forma recursiva. Vamos a ver un ejemplo simple: mostrar todos los elementos de un vector de enteros. Suponed que tenemos un vector de valores enteros, finalizado por un valor -1 que marca el final de la secuencia. Si lo planteáramos como un algoritmo **iterativo**, tendríamos:
|
||||
|
||||
```alg
|
||||
action writeVector(in v: vector of integer)
|
||||
var
|
||||
i: integer
|
||||
end var
|
||||
|
||||
i := 1
|
||||
|
||||
while v[i] ≠ -1 do
|
||||
writeInteger(v[i]);
|
||||
i := i + 1;
|
||||
end while
|
||||
end action
|
||||
```
|
||||
|
||||
```c
|
||||
void writeVector(int *v){
|
||||
int i = 0;
|
||||
|
||||
while (v[i] != -1){
|
||||
printf("%d\n", v[i]);
|
||||
i++;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
Un planteamiento recursivo sería mostar el primer elemento de la secuencia y luego volver a llamar el método recursivo para mostrar el resto de los elementos. Vamos procesando cada elemento de la secuencia (en este caso simplemente mostrar) hasta llegar al elemento que nos marca el final de la secuencia. Para convertirlo en recursivo, hay que buscar la repetición de un patrón, por ejemplo, imaginemos que tenemos el siguiente vector:
|
||||
|
||||
```
|
||||
{1, 2, 3, 4, -1}
|
||||
```
|
||||
|
||||
La llamada
|
||||
|
||||
```c
|
||||
writeVector({1, 2, 3, 4, -1})
|
||||
```
|
||||
|
||||
es equivalente a
|
||||
|
||||
```c
|
||||
writeInteger({2, 3, 4, -1});
|
||||
```
|
||||
|
||||
Por lo tanto, vemos que podemos dividir el problema en otro más simple (es una parte del problema inicial). Además tenemos un caso trivial, que es `writeInteger({-1})` en el que no hay que hacer nada, ya que tenemos un vector sin ningún elemento para mostrar. Por lo tanto, podemos definir una versión recursiva de la función `writeVector`.
|
||||
|
||||
Vamos a ver dos versiones para implementar este algoritmo, una con el uso de **funciones auxiliares** y otra con **punteros**.
|
||||
|
||||
|
||||
#### 20.3.1. Funciones auxiliares
|
||||
|
||||
En algunos casos, el planteamiento recursivo requiere introducir información adicional para poder controlar la recursividad. Para añadir esta informacióin será necesario creqar una nueva función o acción con parámetros adicionales. En este caso, vamos a crear una nueva acción `writeVector_aux` que, además del vector, tendrá la primera posición a procesar. La acción `writeVector` asignará los valores iniciales para el proceso recursivo:
|
||||
|
||||
```alg
|
||||
action writeVector_aux(inout v: vector of integer, in i: integer)
|
||||
if v[i] ≠ -1 then
|
||||
writeInteger(v[i]);
|
||||
writeVector_aux(v, i + 1);
|
||||
end if
|
||||
end action
|
||||
|
||||
action writeVector(inout v: vector of integer)
|
||||
writeVector_aux(v, 1);
|
||||
end action
|
||||
```
|
||||
|
||||
```c
|
||||
void writeVector_aux(int *v, int i){
|
||||
if (v[i] != -1){
|
||||
printf("%d\n", v[i]);
|
||||
writeVector_aux(v, i + 1);
|
||||
}
|
||||
}
|
||||
|
||||
void writeVector(int *v){
|
||||
writeVector_aux(v, 0);
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
#### 20.3.2. Punteros
|
||||
|
||||
Otra posibilidad para implementar este algoritmo es el uso de punteros. En el caso concreto de C, podemos aprovechar el hecho de que un vector realmente es un puntero a la primera posición del vector y, por lo tanto, no necesitamos ningún método auxiliar.
|
||||
|
||||
```c
|
||||
void writeVector(int *v){
|
||||
if (*v != -1){
|
||||
printf("%d\n", *v);
|
||||
writeVector(v + 1);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
En este caso, lo que hacemos es mostrar el contenido del puntero (que es lo mismo que `v[0])`) y desplazar el puntero una posición antes de volver a hacer la llamada recursiva.
|
||||
|
||||
|
||||
|
||||
[Volver arriba](#pec-7)
|
||||
|
||||
[Volver a la PEC 6](../PEC6/README.md) | [Volver al índice principal](../README.md)
|
||||
BIN
fundamentos-programacion/PEC7/ejercicios/ejerc01
Executable file
BIN
fundamentos-programacion/PEC7/ejercicios/ejerc01
Executable file
Binary file not shown.
36
fundamentos-programacion/PEC7/ejercicios/ejerc01.c
Normal file
36
fundamentos-programacion/PEC7/ejercicios/ejerc01.c
Normal file
@@ -0,0 +1,36 @@
|
||||
#include <stdio.h>
|
||||
|
||||
// Definición de constantes
|
||||
#define MAX_NUM 3
|
||||
|
||||
// Función recursiva funcRec
|
||||
int funcRec(int intVec[MAX_NUM], int vectorLength)
|
||||
{
|
||||
int result = 1;
|
||||
|
||||
if (vectorLength > 0)
|
||||
{
|
||||
result *= intVec[vectorLength - 1];
|
||||
result *= funcRec(intVec, vectorLength - 1);
|
||||
}
|
||||
|
||||
return result;
|
||||
}
|
||||
|
||||
// Función principal (main)
|
||||
int main()
|
||||
{
|
||||
int numVec[MAX_NUM];
|
||||
int i;
|
||||
|
||||
// Inicialización del vector numVec
|
||||
for (i = 0; i < MAX_NUM; ++i)
|
||||
{
|
||||
numVec[i] = i + 1;
|
||||
}
|
||||
|
||||
// Llamada a funcRec y escritura del resultado
|
||||
printf("Result: %d\n", funcRec(numVec, MAX_NUM));
|
||||
|
||||
return 0;
|
||||
}
|
||||
BIN
fundamentos-programacion/PEC7/ejercicios/ejerc02
Executable file
BIN
fundamentos-programacion/PEC7/ejercicios/ejerc02
Executable file
Binary file not shown.
34
fundamentos-programacion/PEC7/ejercicios/ejerc02.c
Normal file
34
fundamentos-programacion/PEC7/ejercicios/ejerc02.c
Normal file
@@ -0,0 +1,34 @@
|
||||
#include <stdio.h>
|
||||
|
||||
// Función recursiva funcRec
|
||||
int funcRec(int n)
|
||||
{
|
||||
int sum;
|
||||
|
||||
if (n == 0)
|
||||
{
|
||||
sum = 0;
|
||||
}
|
||||
else
|
||||
{
|
||||
if (n % 2 == 0)
|
||||
{
|
||||
sum = n + funcRec(n - 1);
|
||||
}
|
||||
else
|
||||
{
|
||||
sum = funcRec(n - 1);
|
||||
}
|
||||
}
|
||||
|
||||
return sum;
|
||||
}
|
||||
|
||||
// Función principal (main)
|
||||
int main()
|
||||
{
|
||||
// Llamada a funcRec con argumento 8 y escritura del resultado
|
||||
printf("Result: %d\n", funcRec(8));
|
||||
|
||||
return 0;
|
||||
}
|
||||
BIN
fundamentos-programacion/PEC7/ejercicios/ejerc03
Executable file
BIN
fundamentos-programacion/PEC7/ejercicios/ejerc03
Executable file
Binary file not shown.
27
fundamentos-programacion/PEC7/ejercicios/ejerc03.c
Normal file
27
fundamentos-programacion/PEC7/ejercicios/ejerc03.c
Normal file
@@ -0,0 +1,27 @@
|
||||
#include <stdio.h>
|
||||
|
||||
// Función recursiva mystery
|
||||
int mystery(int a, int b)
|
||||
{
|
||||
if (b == 1)
|
||||
{
|
||||
return a;
|
||||
}
|
||||
else
|
||||
{
|
||||
return (2 * a + mystery(a, b - 1));
|
||||
}
|
||||
}
|
||||
|
||||
// Función principal (main)
|
||||
int main()
|
||||
{
|
||||
int x = 10; // Definición de x
|
||||
int y = 4; // Definición de y
|
||||
int result; // Definición de result
|
||||
|
||||
result = mystery(x, y); // Llamada a mystery con argumentos x e y
|
||||
printf("Result: %d\n", result); // Impresión del resultado
|
||||
|
||||
return 0;
|
||||
}
|
||||
BIN
fundamentos-programacion/PEC7/ejercicios/ejerc04
Executable file
BIN
fundamentos-programacion/PEC7/ejercicios/ejerc04
Executable file
Binary file not shown.
51
fundamentos-programacion/PEC7/ejercicios/ejerc04.c
Normal file
51
fundamentos-programacion/PEC7/ejercicios/ejerc04.c
Normal file
@@ -0,0 +1,51 @@
|
||||
#include <stdio.h>
|
||||
|
||||
// Declaración de funciones
|
||||
int rec(int num1, int num2);
|
||||
int rec2(int num1, int num2);
|
||||
|
||||
// Función recursiva rec
|
||||
int rec(int num1, int num2)
|
||||
{
|
||||
int n;
|
||||
|
||||
if (num2 == 0)
|
||||
{
|
||||
n = num1;
|
||||
}
|
||||
else
|
||||
{
|
||||
n = rec(num2, num1 % num2);
|
||||
}
|
||||
|
||||
return n;
|
||||
}
|
||||
|
||||
// Función rec2 que utiliza rec
|
||||
int rec2(int num1, int num2)
|
||||
{
|
||||
int n;
|
||||
|
||||
n = rec(num1, num2);
|
||||
|
||||
return num1 * num2 / n;
|
||||
}
|
||||
|
||||
// Función principal (main)
|
||||
int main()
|
||||
{
|
||||
int num1, num2;
|
||||
int result;
|
||||
|
||||
printf("Input num1: ");
|
||||
scanf("%d", &num1);
|
||||
|
||||
printf("Input num2: ");
|
||||
scanf("%d", &num2);
|
||||
|
||||
result = rec2(num1, num2);
|
||||
|
||||
printf("Result: %d\n", result);
|
||||
|
||||
return 0;
|
||||
}
|
||||
BIN
fundamentos-programacion/PEC7/ejercicios/ejerc05
Executable file
BIN
fundamentos-programacion/PEC7/ejercicios/ejerc05
Executable file
Binary file not shown.
32
fundamentos-programacion/PEC7/ejercicios/ejerc05.c
Normal file
32
fundamentos-programacion/PEC7/ejercicios/ejerc05.c
Normal file
@@ -0,0 +1,32 @@
|
||||
#include <stdio.h>
|
||||
|
||||
// Declaración de función recursiva
|
||||
int rec(int num1, int num2, int n);
|
||||
|
||||
// Función recursiva rec
|
||||
int rec(int num1, int num2, int n)
|
||||
{
|
||||
if (num1 >= num2)
|
||||
{
|
||||
n = rec(num1 - num2, num2, n + 1);
|
||||
}
|
||||
return n;
|
||||
}
|
||||
|
||||
// Función principal (main)
|
||||
int main()
|
||||
{
|
||||
int num1, num2, n = 0;
|
||||
|
||||
printf("Input num1: ");
|
||||
scanf("%d", &num1);
|
||||
|
||||
printf("Input num2: ");
|
||||
scanf("%d", &num2);
|
||||
|
||||
int result = rec(num1, num2, n);
|
||||
|
||||
printf("Result: %d\n", result);
|
||||
|
||||
return 0;
|
||||
}
|
||||
BIN
fundamentos-programacion/PEC7/ejercicios/ejerc06
Executable file
BIN
fundamentos-programacion/PEC7/ejercicios/ejerc06
Executable file
Binary file not shown.
35
fundamentos-programacion/PEC7/ejercicios/ejerc06.c
Normal file
35
fundamentos-programacion/PEC7/ejercicios/ejerc06.c
Normal file
@@ -0,0 +1,35 @@
|
||||
#include <stdio.h>
|
||||
|
||||
// Declaración de función recursiva
|
||||
int x(int n);
|
||||
|
||||
// Función recursiva x
|
||||
int x(int n)
|
||||
{
|
||||
if (n <= 1)
|
||||
{
|
||||
return n;
|
||||
}
|
||||
else
|
||||
{
|
||||
return x(n - 1) + x(n - 2);
|
||||
}
|
||||
}
|
||||
|
||||
// Función principal (main)
|
||||
int main()
|
||||
{
|
||||
int n;
|
||||
|
||||
n = 1;
|
||||
|
||||
while (n <= 5)
|
||||
{
|
||||
printf("%d ", x(n));
|
||||
n = n + 1;
|
||||
}
|
||||
|
||||
printf("\n");
|
||||
|
||||
return 0;
|
||||
}
|
||||
BIN
fundamentos-programacion/PEC7/ejercicios/ejerc07
Executable file
BIN
fundamentos-programacion/PEC7/ejercicios/ejerc07
Executable file
Binary file not shown.
34
fundamentos-programacion/PEC7/ejercicios/ejerc07.c
Normal file
34
fundamentos-programacion/PEC7/ejercicios/ejerc07.c
Normal file
@@ -0,0 +1,34 @@
|
||||
#include <stdio.h>
|
||||
|
||||
// Declaración de funciones
|
||||
int rec(char char1, int n);
|
||||
char codeToChar(int code);
|
||||
int charToCode(char c);
|
||||
|
||||
// Función recursiva rec
|
||||
int rec(char char1, int n) {
|
||||
if (char1 > 'a') {
|
||||
n = rec(codeToChar(charToCode(char1) - 1), n + 1);
|
||||
}
|
||||
return n;
|
||||
}
|
||||
|
||||
// Función para convertir código a caracter
|
||||
char codeToChar(int code) {
|
||||
return (char)code;
|
||||
}
|
||||
|
||||
// Función para convertir caracter a código
|
||||
int charToCode(char c) {
|
||||
return (int)c;
|
||||
}
|
||||
|
||||
// Algoritmo principal
|
||||
int main() {
|
||||
char char1 = 'c';
|
||||
int n = 0;
|
||||
|
||||
printf("Result: %d\n", rec(char1, n));
|
||||
|
||||
return 0;
|
||||
}
|
||||
@@ -775,3 +775,5 @@ action writeBoolean(in varName: boolean);
|
||||
|
||||
|
||||
[Volver arriba](#pr-1)
|
||||
|
||||
[Volver a la PEC3](../PEC3/README.md) | [Seguir a la PEC 4](../PEC4/README.md)
|
||||
|
||||
@@ -1164,5 +1164,6 @@ algorithm main
|
||||
end algorithm
|
||||
```
|
||||
|
||||
|
||||
[Volver arriba](#pr-2)
|
||||
|
||||
[Volver a la PEC4](../PEC4/README.md) | [Seguir a la PEC 5](../PEC5/README.md)
|
||||
|
||||
@@ -1509,3 +1509,5 @@ end algorithm
|
||||
|
||||
|
||||
[Volver arriba](#pr-3)
|
||||
|
||||
[Volver a la PEC5](../PEC5/README.md) | [Seguir a la PR 4](../PR4/README.md)
|
||||
|
||||
@@ -311,3 +311,5 @@ Tener en cuenta que:
|
||||
|
||||
|
||||
[Volver arriba](#pr-4)
|
||||
|
||||
[Volver a la PR3](../PR3/README.md) | [Seguir a la PEC 6](../PEC6/README.md)
|
||||
|
||||
@@ -35,10 +35,12 @@ Aquí dejaré los apuntes de la asignatura "Fundamentos de la programación" de
|
||||
- [PR 3](./PR3/README.md#pr-3)
|
||||
- [16. Tipos de datos estructurados: tabla](./PR3/README.md#16-tipos-de-datos-estructurados-tabla)
|
||||
|
||||
- [PR4](./PR4/README.md#pr-4)
|
||||
- [PR 4](./PR4/README.md#pr-4)
|
||||
- [17. Esquemas de recorrido y búsqueda](./PR4/README.md#17-esquemas-de-recorrido-y-búsqueda)
|
||||
|
||||
- [PEC 6](./PEC6/README.md#pec-6)
|
||||
- [18. Tipos abstractios de datos](./PEC6/README.md#18-tipos-abstractios-de-datos)
|
||||
- - [19. Navegación de TAD](./PEC6/README.md#19-navegación-de-tad)
|
||||
- [19. Navegación de TAD](./PEC6/README.md#19-navegación-de-tad)
|
||||
|
||||
- [PEC 7](./PEC7/README.md#pec-7)
|
||||
- [20. Recursividad](./PEC7/README.md#20-recursividad)
|
||||
|
||||
Reference in New Issue
Block a user